Getting Started

These are some basic ideas on how to write Punctual code, and its syntax.

Writing and running an expression

You have several options in order to run Punctual code:

• Standalone web editor. It’s immediate to use, and the screen is clean to show in a live performance.
• Estuary. Nearly as immediate to use, and it offers the possibility to use more than one live-coding language at the same time, and to collaborate with other people online. It also has some integrated help and tutorials. It’s a bit more work to get a completely clean screen to show it in a live performance. See the github repository and this unofficial Estuary reference for more information on how to configure and use Estuary.
• Download Punctual standalone. You can get the last Punctual version from the release section of the official github repository. This is the same as the first option, but you won’t need an Internet connection in order to use it, so it’s ideal in a live performance at a venue where you don’t know if you would have any connectivity at all.
• Download and compile Estuary. It’s also possible to get a local copy of Estuary to use off-line, but in this case you need to compile the source code yourself. You can clone the Estuary github repository and follow the instructions in BUILDING.md. Compiling Estuary isn’t an easy task and it’s unnecessary on most cases.

If you are new to Punctual, choose any of the two first options and go ahead.

Once you are able to try Punctual, just write or paste the expression you want to execute and run it pressing Shift+Enter. In Estuary, you also have a “play” button.

Commenting out

When using Punctual (or any other live-coding language), you’ll usually need a way to comment out parts of the code, to avoid running them.

You can do this in Punctual by appending -- in front of the line you want to comment, or by using the function zero that will convert any graph to a blank screen.

It’s also possible to comment out multiple lines by enclosing them between {- and -} markers.

Often, when playing with visuals, you’ll end up with a completely white screen and no easy way to see your code. The easiest way to recover control is by selecting all your code with Ctrl+A (Cmnd+A in MacOS), deleting it all (Del), and running the result (Shift+Enter). This is a fast way to remove all visuals and recover a blank screen. Now, you can recover your old code by undoing your last operation (Ctrl+Z or Cmnd+Z) and modify it before running it again.

Notes on Haskell

Punctual is written using the programming language Haskell, and inherits some of its syntax. This is a short summary of some syntactic details that are important:

Negative numbers

In some contexts, negative numbers need to be surrounded by parentheses. That is because - is also an operator, and sometimes the compiler may have problems distinguishing between the negative sign and the minus operator.

-fx >> add; -- error
-1*fx >> add; -- error
(-1)*fx >> add; -- correct

spin [-pi] fx >> add; -- error
spin [(-1)*pi] fx >> add; -- correct

Parentheses () and dollar $

The space character is the parameter separator both in Haskell and in Punctual. This can lead to some confusion when nesting various functions:

-- Error: the compiler can't tell what numbers are arguments to circle and what to vline:
vline circle 0 0.1 0.1 >> add;

You can use parentheses to clearly indicate how this expression needs to be interpreted:

vline (circle 0 0.1) 0.1 >> add;

In longer statements, using parentheses may become tedious and prone to errors:

spin (saw [-0.13,0.13]) (move [-0.2,0,0.2,0] (circle 0 0.1)) >> add;

The dollar ($) operator can be used to substitute a pair of parentheses. It indicates that all things that follow are to be executed before, so it’s equivalent to enclosing with parentheses all that follows.

The previous expression can be rewritten like this:

spin (saw [-0.13,0.13]) $ move [-0.2,0,0.2,0] $ circle 0 0.1 >> add;

This is a faster and clearer way to write this type of expression. Note that there is only a pair of parentheses remaining, that we can’t substitute by a dollar, as saw [-0.13,0.13] is not the last argument of spin:

-- Error: this two expressions are equivalent (and don't make sense, as spin is lacking an argument):
spin $ saw [-0.13,0.13] $ move [-0.2,0,0.2,0] $ circle 0 0.1 >> add;
spin (saw [-0.13,0.13] (move [-0.2,0,0.2,0] (circle 0 0.1))) >> add;

Lists

Lists are a very used data type both in Haskell and in Punctual. They are written between square brackets, and their elements separated by commas:

circle [0,0.3,0.5,0.2,-0.3,-0.1] 0.2 >> add;

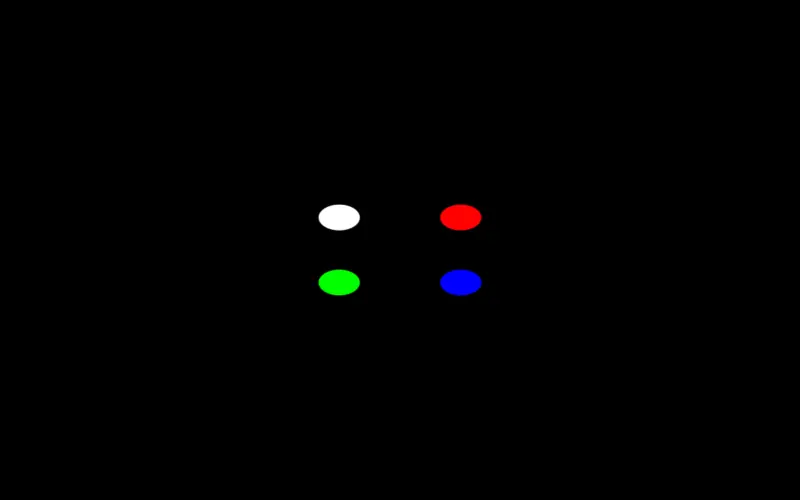
[unipolar fx, 0.4, osc 0.1] >> add;

List expansion

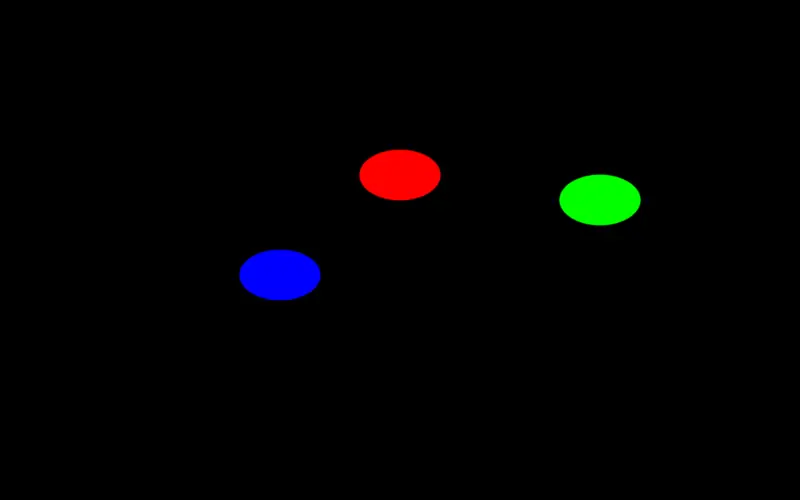
As seen in channels, we can use many values in a Punctual expression, and they will be expanded into a complexer graph. For example, circle [-0.5,0,0.5,0] 0.2 >> add; will draw two circles, one red and one cyan.

If you want to create more objects in a statement like this, it can quickly get tedious to write all the numbers.

Here is where Haskell syntax for expanding lists becomes useful.

All you have to write to expand a list is the first and second values, followed by two dots (..) and the limit:

l << [0,0.1 .. 0.5];
--l << [0,0.1,0.2,0.3,0.4,0.5];
hline l 0.01 >> add;

Note that these two versions of l are equivalent, and the limit 0.5 is included.

This works fine with hline as we only need the y-coordinate to write a horizontal line.

Combining lists

If we want to use the same trick with point or circle, we’ll need to provide pairs of coordinates.

With zip we can build all the x-coordinates in a list, then all the y-coordinates in another list, and finally join them:

xs << [-0.4,-0.3 .. 0.4];
--xs << [-0.4,-0.3,-0.2,-0.1,0,0.1,0.2,0.3,0.4];
ys << [0,0.1 .. 0.8];
--ys << [0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8];
circle (zip xs ys) 0.05 >> add;

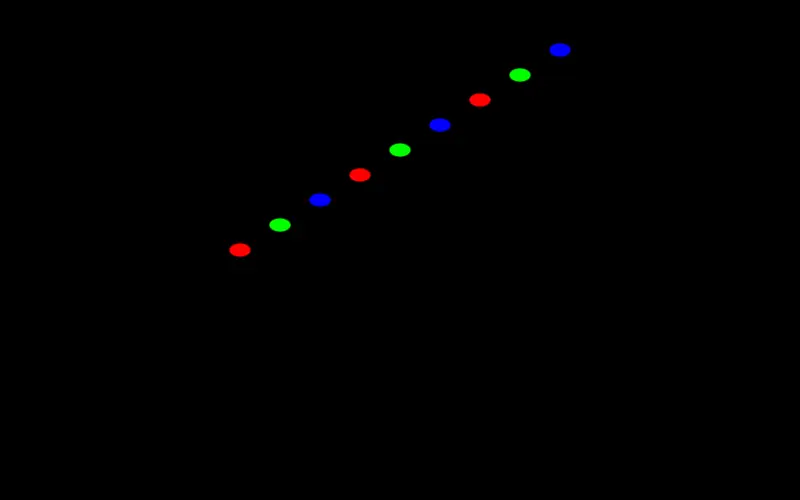
When using zip, if one input list is shorter than the other, excess elements of the longer list are discarded.

Another way to combine lists is by putting them one after the other in a new list:

xs << [0,0.1 .. 0.7];
ys << [-0.3,-0.2 .. 0.3];
circle [xs,ys] 0.05 >> add;

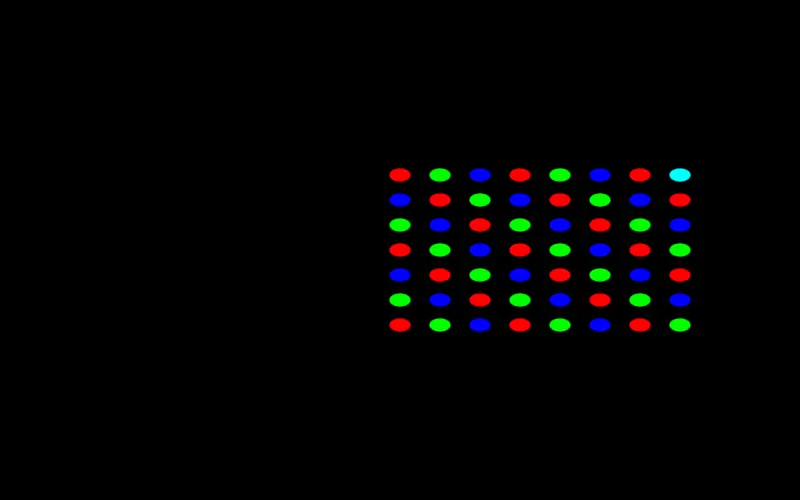
Note that this creates a list with all possible combinations of one element from the first list and one element of the second list.

What if you want a set of circles with distinct x-coordinates, but at the same height? Punctual automatically expands single numbers to lists if necessary, so you can do this:

xs << [-0.95,-0.9 .. 0.95];
ys << 0;
fit 1 $ circle [xs,ys] 0.05 >> add;

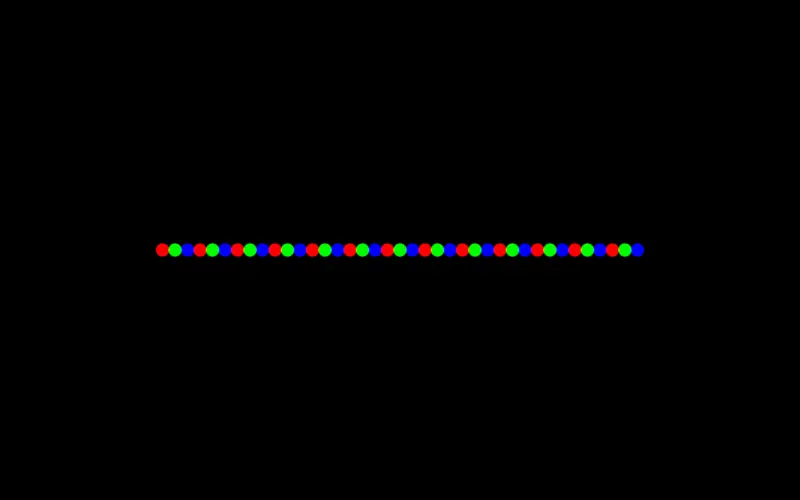
The last way you have to combine two lists is by simply appending one after the other. This is just what the operator ++ does, so for example, [1,2,3,4]++[5,6,7] results in [1,2,3,4,5,6,7].

l1 << [-0.9,-0.83 .. -0.3];
l2 << [0.9,0.83 .. 0.3];
circle [l1++l2,0] 0.05 >> add;

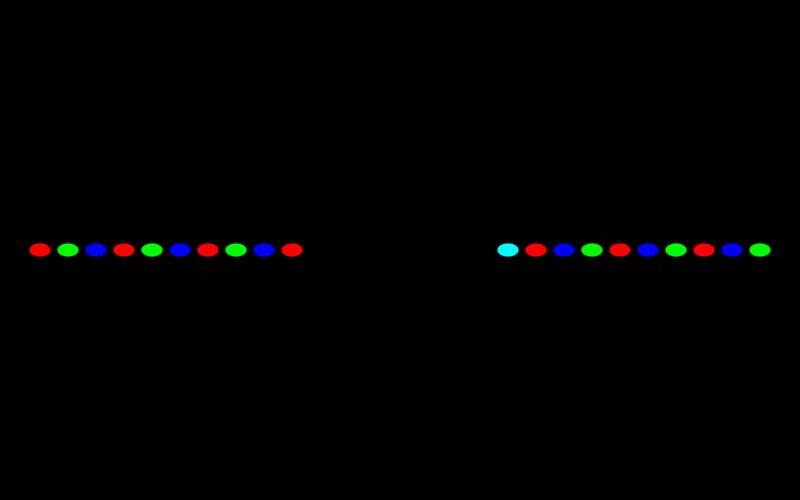
Now, remember that in Punctual all things are really graphs. So, using any of these to combine lists is only a very particular case of what can be done.

For example, using ++ we can join two graphs:

c << circle 0 0.2;
l << hline 0 0.05;
c++l >> add;

And here we can see what is really happening: the two graphs are joined and the result has the sum of the channels of the first and the second input graphs. In our case, these are 1 and 1, so the result has 2 channels, hence the colors (see output notations if this isn’t clear).

See combining graphs and combining channels for more information and examples on how to combine graphs and channels.